Hello folks, recently I participated in the 1st Pakistan Cyber Security Challenge CTF. My team secured 1st position in the qualifying round and came in 2nd place in the final round held at Air University, Islamabad. It was a wonderful experience, the challenges were well-designed, and Team AirOverflow is to be commended for their efforts.
All of the cryptography challenges from the qualifier and final rounds will be discussed in detail in this write-up.
Qualifier Round
Baquette
The french make excellent cuisine. Well, even stronger encryption schemes. Do you really think you can fully eat this baquette?
Key: auctf
1
2
3
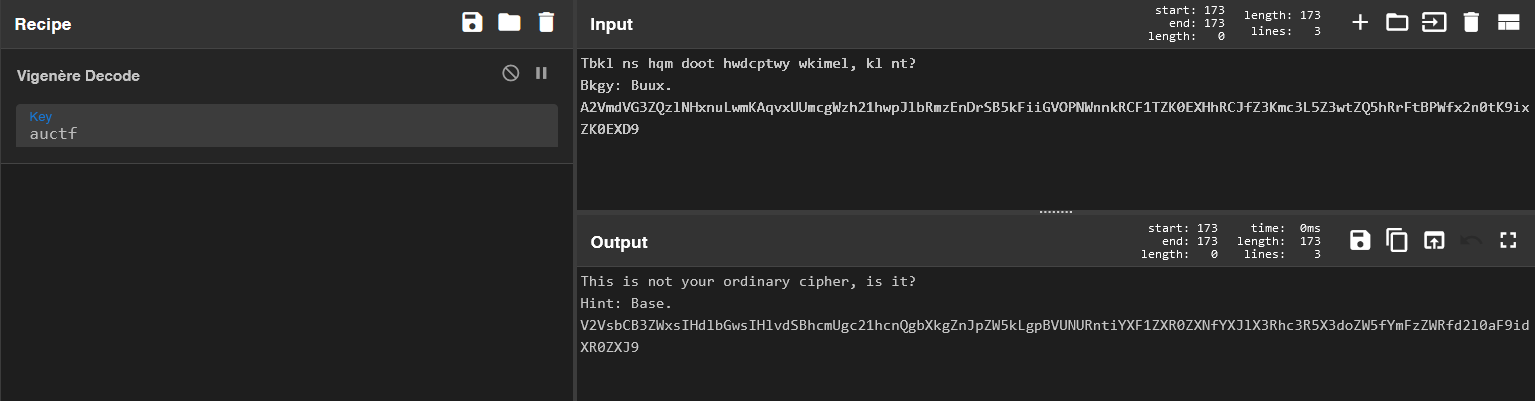
Tbkl ns hqm doot hwdcptwy wkimel, kl nt?
Bkgy: Buux.
A2VmdVG3ZQzlNHxnuLwmKAqvxUUmcgWzh21hwpJlbRmzEnDrSB5kFiiGVOPNWnnkRCF1TZK0EXHhRCJfZ3Kmc3L5Z3wtZQ5hRrFtBPWfx2n0tK9ixZK0EXD9
The inclusion of the French in the challenge description suggests that this is the well-known Vigenere Cipher, since it was created in France. The key has been provided, so let’s open CyberChef and enter the ciphertext and key.
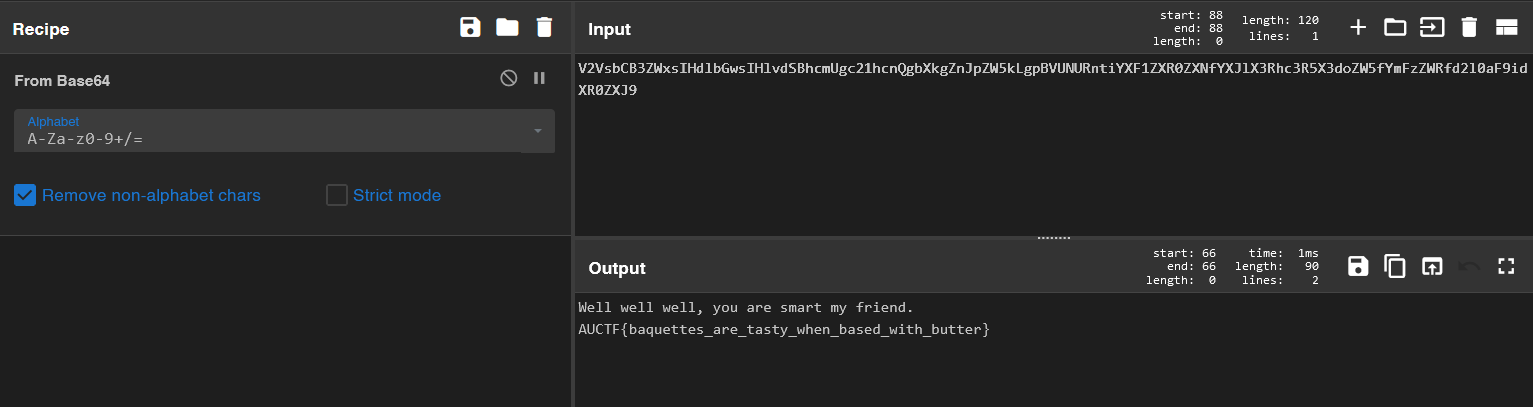
The plaintext yields another ciphertext which appears to be base64 encoded, we can decode it using CyberChef.
And we got the flag!
Flag: AUCTF{baquettes_are_tasty_when_based_with_butter}
Climber
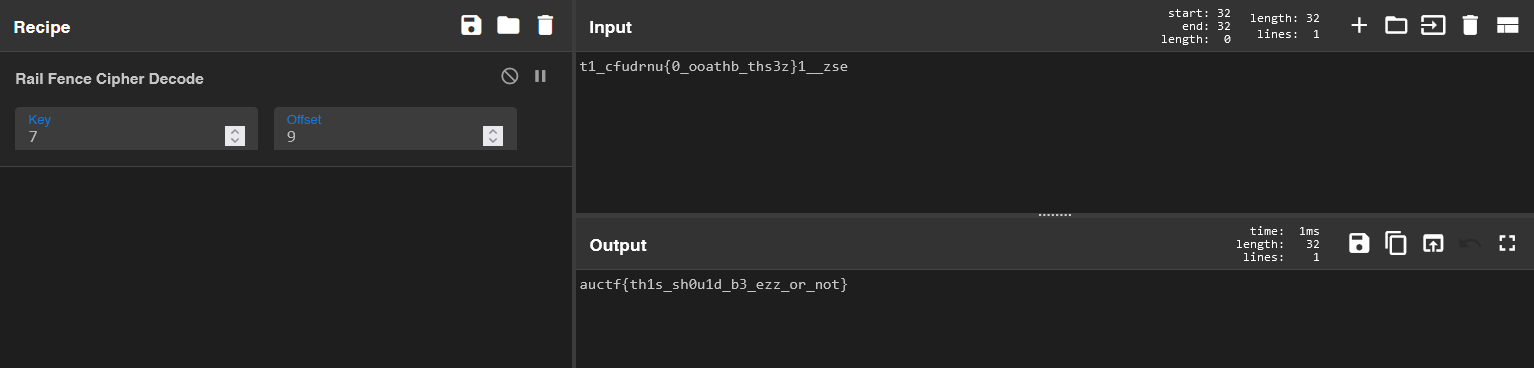
Have you ever seen someone who is 7 feet tall, fencing on a 5-10 feet long railing? Well, me neither.
t1_cfudrnu{0_ooathb_ths3z}1__zse
The Rail Fence Cipher is referenced in the challenge description, with 7 being the key and offset between 5 and 10. So let’s test all five key-offset pairs on CyberChef. On 7 as key 9 as offset we obtain the correct plaintext.
Flag: auctf{th1s_sh0u1d_b3_ezz_or_not}
RSA
Cipher
1
2
3
n = 31436211274852062801590948458671058204728701377920047195870016302697956796267506278727106968536534553505650010973423533569252216811398069950057574348601027314737123
e = 65537
c = 22840372395669361935504971154513566142872479734989306848229554805124371541157041389213350875178287707977731738003789623205786790284199917036685723196756139847839346
Solution
This is an RSA challenge, as the name implies. We are given the ciphertext ct as well as the public key (n, e), where n is a product of two unknown primes p and q and e is the public exponent.
According to Wikipedia, the difficulty of dividing the modulus n into its prime parts p and q determines the security of RSA and as of 2020, the largest publicly known broken RSA key is RSA-250, which has 829 bits.
Meanwhile, the supplied n value is just 544 bits long and hence easily factorable. Let’s write a python script that factors n to p and q.
Now that we have the values of p and q, the rest of the solution is basically textbook RSA, in which we compute the value of phi and then its private exponent d by:
Finally, decrypt the ciphertext by computing
\[plaintext = c^d\ mod\ n\]Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
from Crypto.Util.number import *
from sympy.ntheory import factorint
n = 31436211274852062801590948458671058204728701377920047195870016302697956796267506278727106968536534553505650010973423533569252216811398069950057574348601027314737123
e = 65537
c = 22840372395669361935504971154513566142872479734989306848229554805124371541157041389213350875178287707977731738003789623205786790284199917036685723196756139847839346
p, q = factorint(n)
phi = (p - 1) * (q - 1)
d = inverse(e, phi)
pt = pow(c, d, n)
print(long_to_bytes(pt))
Flag: auctf{l4st_FLAG}
Kin
In this challenge, we are given an encryption function and a list of the decimal equivalents of the encrypted flag’s bytes.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import random
flag = REDACTED
def encrypt(data):
mod = 256
a = 203
b = random.randint(1,mod)
res = []
for i in data:
enc = (a*ord(i) + b) % mod
res.append(enc)
return res
print(encrypt(flag))
# flag = [152, 116, 46, 169, 143, 54, 152, 143, 143, 136, 231, 196, 2, 136, 222, 2, 99, 19, 30, 152, 134, 152, 99, 81, 196, 204]
It appears that the encryption function is akin to that of the Affine Cipher, hence the name Kin.
The encryption function for a single letter x in mathematical notation is
where a and b are the keys, and m is the number of letters in the character set, which in ASCII is 256. The values for a and m are known, but the value of b is picked at random from a range of 1...256, which we can easily brute-force.
The decryption function for a single letter x is
where $a^{-1}$ is the modular multiplicative inverse of a modulo m. We can find its value using invert function from the gmpy2 library.
Let’s now write the decryption function and recover the plaintext.
1
2
3
4
5
6
7
8
9
def decryption(msg):
for b in range(256): # brute-forcing the value for b
pt = ""
for char in msg:
char = 227 * (char - b) % 256
pt += chr(char)
if "auctf" in pt:
print(pt)
break
Flag: auctf{aff1ne_1s_br3akable}
Associative
1
2
3
What matters is if A==B then B==A.
CIPHER_TEXT = ExQNEAkWEwoLOV5HPBUVK3QQDEIRXwQEEw== KEY = cmFuZG9ta2V5Zm9yY3RmWERzZXZlbg==
Solution
The use of the word Associative and the suggestion of a one-to-one relation between A and B indicate that plaintext is subjected to a straightforward XOR operation. Because XOR is associative, if $a \oplus b = c$, then $b \oplus c = a$, and similarly $a \oplus c = b$.
Both the ciphertext and the key were encoded using base64, therefore we must first decode them to their original byte form before recovering the plaintext by conducting a bitwise XOR operation on the ciphertext and key.
1
2
3
4
5
6
7
8
9
10
from pwn import *
import base64
CIPHER_TEXT = "ExQNEAkWEwoLOV5HPBUVK3QQDEIRXwQEEw=="
KEY = "cmFuZG9ta2V5Zm9yY3RmWERzZXZlbg=="
cipher_text = base64.b64decode(CIPHER_TEXT)
key = base64.b64decode(KEY)
print(xor(cipher_text, key))
Flag: auctf{xor_15_ass0ci4t1ve}
Final Round
Write34
1
2
3
4
5
6
7
8
9
10
11
12
13
flag = flag.encode()
for i in range(3):
flag = base64.b16encode(flag)
flag = base64.b32encode(flag)
flag = base64.b64encode(flag)
fernet = Fernet(key)
for i in range(3):
flag = fernet.encrypt(flag)
for i in range(3):
flag = binascii.hexlify(flag)
Attachments:
For this challenge, we’re provided with a custom encryption algorithm that first encodes the flag three times using base16, base32, and base64. The algorithm then utilizes fernet to encrypt the flag three times, and finally, and the flag is then converted to hex three times.
The solution is fairly simple, all that needs to be done to recover the plaintext is to reverse the algorithm since we already know the key and the ciphertext.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
from binascii import unhexlify
from cryptography.fernet import Fernet
import base64
flag = open("flag.txt").read()
key = "YntAd4Y6MNT0uRgfsHnagRPXux7Hgs0lwIjKbrd8MbQ="
fernet = Fernet(key)
for i in range(3):
flag = unhexlify(flag)
for i in range(3):
flag = fernet.decrypt(flag)
for i in range(3):
flag = base64.b64decode(flag)
flag = base64.b32decode(flag)
flag = base64.b16decode(flag)
print(flag)
Flag: AUCTF{suCh_3nc0d1ng_muCh_fl4g_w0w}
BiggiE small :D
Last time our RSA encryption was weak, a mathematician suggested to increase the exponent, because more bits makes it more secure.
1
2
n: 609983533322177402468580314139090006939877955334245068261469677806169434040069069770928535701086364941983428090933795745853896746458472620457491993499511798536747668197186857850887990812746855062415626715645223089415186093589721763366994454776521466115355580659841153428179997121984448771910872629371808169183
e: 387825392787200906676631198961098070912332865442137539919413714790310139653713077586557654409565459752133439009280843965856789151962860193830258244424149230046832475959852771134503754778007132465468717789936602755336332984790622132641288576440161244396963980583318569320681953570111708877198371377792396775817
Attachments:
It is an RSA challenge, and the description suggests that a big public exponent is used. Looking at the public key, it can be seen that the value of e is too big, which is unusual. A quick google search reveals that having an unusually big value for the public exponent results in a small value for the private exponent d, which makes RSA prone to Weiner’s Attack. Read in detail from Twenty Years of Attacks on the RSA Cryptosystem.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
from Crypto.Util.number import *
def wiener(e, n):
# Convert e/n into a continued fraction
cf = continued_fraction(e/n)
convergents = cf.convergents()
for kd in convergents:
k = kd.numerator()
d = kd.denominator()
# Check if k and d meet the requirements
if k == 0 or d%2 == 0 or e*d % k != 1:
continue
phi = (e*d - 1)/k
# Create the polynomial
x = PolynomialRing(RationalField(), 'x').gen()
f = x^2 - (n-phi+1)*x + n
roots = f.roots()
# Check if polynomial as two roots
if len(roots) != 2:
continue
# Check if roots of the polynomial are p and q
p,q = int(roots[0][0]), int(roots[1][0])
if p*q == n:
return d
return None
# Test to see if our attack works
if __name__ == '__main__':
n = 609983533322177402468580314139090006939877955334245068261469677806169434040069069770928535701086364941983428090933795745853896746458472620457491993499511798536747668197186857850887990812746855062415626715645223089415186093589721763366994454776521466115355580659841153428179997121984448771910872629371808169183
e = 387825392787200906676631198961098070912332865442137539919413714790310139653713077586557654409565459752133439009280843965856789151962860193830258244424149230046832475959852771134503754778007132465468717789936602755336332984790622132641288576440161244396963980583318569320681953570111708877198371377792396775817
d = wiener(e,n)
c_bytes = open("flag.enc", "rb").read()
c = bytes_to_long(c_bytes)
pt = pow(c, d, n)
print(long_to_bytes(int(pt)))
Flag: auctf{huge_e_small_d_and_wiener_attack}
We can mark the challenge as solved here. However, there’s another, unintended way to solve this challenge. The modulus used by the challenge author is quite old, and can easily be factorized into p and q using factordb.com.
Rest is textbook RSA, we can simply follow the same steps as we did in the RSA challenge from the qualifier round. However, the flag.enc consists of bytes rather than long integer this time, so we will use the bytes_to_long function of pycryptodome library to convert the ciphertext to a long integer.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
from Crypto.Util.number import *
n = 609983533322177402468580314139090006939877955334245068261469677806169434040069069770928535701086364941983428090933795745853896746458472620457491993499511798536747668197186857850887990812746855062415626715645223089415186093589721763366994454776521466115355580659841153428179997121984448771910872629371808169183
e = 387825392787200906676631198961098070912332865442137539919413714790310139653713077586557654409565459752133439009280843965856789151962860193830258244424149230046832475959852771134503754778007132465468717789936602755336332984790622132641288576440161244396963980583318569320681953570111708877198371377792396775817
flag = open("flag.enc", "rb").read()
ct = bytes_to_long(flag)
# from factordb
p = 22107961593273663554447672179167919592270857343971618325649212520279122827566022270428817505638791153667398184068987608971763363269212331920067006335889541
q = 27591125068163886831989228774178759832120484388897183929367433612315983402979538404952530012269465045393978140179601040530392691765067542341015115680614163
phi = (p - 1) * (q - 1)
d = inverse(e, phi)
pt = pow(ct, d, n)
print(long_to_bytes(pt))
Flag: auctf{huge_e_small_d_and_wiener_attack}
555
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
import random
from Crypto.Util.number import long_to_bytes
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad
bits = 128
shares = 30
## pardon my bad coding practices
## improvise adapt dryrun
def encrypt(flag):
key = random.randbytes(16)
cipher = AES.new(key, AES.MODE_ECB)
enc_flag = cipher.encrypt(pad(flag, 16))
f = open("flag4.enc", "w")
return enc_flag.hex()
poly = [random.getrandbits(bits) for _ in range(shares)]
flag = open("./flag4.txt", "rb").read()
random.seed(poly[0])
print(encrypt(flag))
x = int(input("input x: "))
print(sum(map(lambda i: poly[i] * pow(x, i), range(len(poly)))))
We are provided with a Python code that generates a random array of size 30, then uses the first element as a seed to the random function. The encryption function is then called, which produces a random key and encrypts the flag with AES.
I was unable to solve this challenge during the event, since the challenge required some time to tinker with it, and an understanding of positional number system. And I lacked both 🤡.
The encryption function is straightforward. AES with ECB mode is used, and a random key of 16 bytes is created. Line 22 shows the usage of a seed poly[0], which is also generated randomly. The usage of seed ensures that the random function generates the same random integers each time it is run. Once we retrieve the seed’s value, solving this challenge will be a piece of cake.
The program takes input the value of x on line 25 and then, on line 26, loops over the elements of the list poly and sums the product of values on each index of poly array with $x^i$ where i is the iterator.
The last line of code can also be expressed as:
\[\sum_{i=0}^{29} poly_{i} \times x^i\]Or in python:
1
2
3
4
5
6
s = 0
for i in range(len(poly)):
s += poly[i] * pow(x, i)
print(s)
We need to extract poly[0] from the sum. We know that any base to the power 0 is 1 e.g.: \(2^0 = 1\) , and similarly \(0^0 = 1\) .
If we enter x as 0, we can trick the program into doing
For all iterations except \(i=0\), the result of the product will be 0. In case of \(i = 0\), the right hand side of the product will become 1 and the product will be equal to poly[i]. This will only be true because
Hence, the sum will be equal to poly[0]. Now we can simply use it as a seed to generate our key and decrypt the flag.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
from Crypto.Cipher import AES
import random
enc_flag = "f79beca540b155be28b83c8b871640888766c70b82670f2cde28c40976d46fc7"
flag_bytes = bytes.fromhex(enc_flag)
seed = 270882600965622237109048171195266900279 # poly[0] or the sum when x is 0
random.seed(seed)
key = random.randbytes(16)
cipher = AES.new(key, AES.MODE_ECB)
dec_flag = cipher.decrypt(flag_bytes)
print(dec_flag)
Flag: auctf{hash3lizer_ust@@d_<3}
Mathematics, Cryptography, Magic, Mystery, Beauty. That’s all Folks. Have a great day!